Metodos numericos: marzo 2023

jueves, 23 de marzo de 2023

Métodos de interpolación

Llevar a cabo una interpolación lineal es muy simple, solo hay que seguir estos pasos:

Paso 1

Determinar el punto incógnita P(x,y).

Paso 2

Establecer los dos puntos que limitan el intervalo donde se encuentra el valor a calcular, es decir, los puntos (xo,yo) y (x1, y1).

Paso 3

Sustituir todos los valores en la ecuación:

$y=y_{o}+\left [\frac{y_{1}-y_{o}}{x_{1}-x_{o}} \right ]\left (x-x_{o} \right )$

Y calcular el resultado.

Ejemplos de interpolación lineal

Ejemplo 1

Se quiere hallar el valor aproximado de ln 3 a través de una interpolación lineal, dados los siguientes valores:

ln 2 = 0.693147 y ln 4 = 1.386294

Comparar el resultado con el valor de ln 3 obtenido a través de una calculadora y determinar el margen error cometido.

Paso 1

Para encontrar el valor aproximado de ln 3 hay que proceder siguiente modo: en primer lugar se establece la incógnita, que es y = ln 3, junto a su correspondiente valor de “x”: x = 3. Este es el punto que se quiere calcular: (3, ln 3).

Paso 2

Después hay que establecer los puntos límites del intervalo con los valores conocidos. Se pide hacerlo con la siguiente pareja de puntos:

Límite inferior: [xo = 2; yo = ln 2 = 0.693147]
Límite superior: [x1 = 4; y1 = ln 4 = 1.386294]
Paso 3

Los valores determinados en los pasos 1 y 2 se sustituyen cuidadosamente en la ecuación para generar el resultado de la aproximación a ln 3:

Puede servirte: Derivadas parciales: propiedades, cálculo, ejercicios

$y=y_{o}+\left [\frac{y_{1}-y_{o}}{x_{1}-x_{o}} \right ]\left (x-x_{o} \right )$

$ln\: 3= ln\: 2+\left [\frac{ln4-ln2}{4-2} \right ]\left (3-2 \right )$
$ln\: 3= 0.693147+\left [\frac{1.386294-0.693147}{4-2} \right ]\left (3-2 \right )=1.039721$ El valor real de ln 3 obtenido mediante calculadora es:

ln 3 =1.098612

Y el margen de error es:

Error = │1.098612 − 1.03971 │= 0.059

El error porcentual de la interpolación se calcula dividiendo el error entre el valor real de ln3 y multiplicando por 100 %:

Error porcentual = (Error/Valor real)× 100 = (0.059/1.098612)×100% = 5.4%

Ejemplo 2

Ahora se desea hallar el valor aproximado de ln 3 mediante interpolación lineal, conocidos estos dos valores:

ln 2.5 = 0.916291 y ln 3.5 = 1.252763

Determinar también el error correspondiente y comparar con los resultados del ejemplo anterior.

Paso 1

De nuevo el punto incógnita es:

y = ln 3, x = 3

Paso 2
Límite inferior: [xo = 2.5; yo = yo = ln 2.5 = 0.916291]
Límite superior: [x1 = 3.5; y1 = ln 3.5 = 1.252763]
Paso 3

$y=y_{o}+\left [\frac{y_{1}-y_{o}}{x_{1}-x_{o}} \right ]\left (x-x_{o} \right )$

$ln\: 3= ln \: 2.5+\left [\frac{ln\: 3.5-ln \: 2.5}{3.5-2.5} \right ]\left (3-2.5 \right )=1.084527$ Examinando el valor ofrecido por la calculadora:

ln 3 =1.098612

Se determina la cota de error en este caso, que resulta:

Error = │1.098612 − 1.084527 │= 0.014

El error porcentual en este caso es ≈ 1.3 %. Comparando con la cota de error del ejemplo 1, el nuevo valor es más preciso, pues el intervalo elegido para interpolar es menor.

Ejercicios resueltos

Ejercicio 1

Calcular, mediante interpolación lineal, el calor específico del aire a presión constante cp y temperatura de 530 K, partiendo de la tabla de valores que se muestra a continuación.

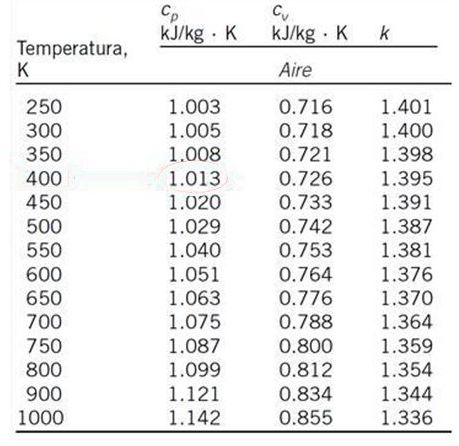
Solución

En la resolución de muchos problemas es frecuente que el valor que se busca no aparezca exactamente como se desea en la tabla de valores que se tiene a mano. Una alternativa es elegir el valor más cercano al deseado, pero muchas veces basta una interpolación lineal para encontrar una aproximación mucho mejor.

El valor de cp a 530 K no aparece en la tabla adjunta, pero se puede hacer una interpolación lineal con los respectivos calores específicos a 500 K y 550 K, que son las temperaturas más cercanas a 530 K y cuyos calores específicos sí aparecen en la tabla mostrada.

Los respectivos calores específicos a presión constante para dichas temperaturas son:

To = 500 K; cpo = 1.029 kJ /kg∙K

T1 = 550 K; cp1 = 1.040 kJ /kg∙K

Y la incógnita es el punto (500K, cp)

Sustituyendo en la fórmula de la interpolación lineal dada anteriormente, con T en el lugar de la variable “x” y cp en lugar de “y”, se tiene:

$y=y_{o}+\left [\frac{y_{1}-y_{o}}{x_{1}-x_{o}} \right ]\left (x-x_{o} \right )$

$c_{p}= c_{po}+\left [\frac{c_{p1}-c_{po}}{T_{1}-T_{o}} \right ]\left (T-T_{o} \right )$

$c_{p}= 1.029+\left [\frac{1.040-1.029}{550-500} \right ]\left (530-500 \right )\frac{kJ}{kg\cdot K}=1.03536\frac{kJ}{kg\cdot K}$

Ejercicio 2

La carga aplicada a un resorte (en kilopondios) produce las siguientes elongaciones (en milímetros) de acuerdo a la tabla que se muestra:

Calcular la elongación cuando la carga es 12.6 kp.

Solución

Sea y el valor de la elongación buscada cuando la carga es C = 12.6 kp. El punto incógnita es (12.6, y), que se encuentra entre los puntos:

Co = 10 kp; yo = 105 mm

C1 = 15 kp; y1 = 172 mm

Solo resta sustituir los valores en la ecuación:

$C= 105+\left [\frac{172-105}{15-10} \right ]\left (12.6-10 \right )\: mm=139.84\: mm$

interpolacion polinomica

interpolacion lineal

Interpolacion de Newton

viernes, 17 de marzo de 2023

Codigo de Aproximaciones sucesivas

package aproximaciones.sucesivas;

import java.util.Scanner;

public class AproximacionesSucesivas {

public static void main(String[] args) {

Scanner leer = new Scanner (System.in);

// - CREACION VARIABLES -

double x1,g1,ep1,raiz,b1;

raiz=5;

// - INTRODUCCION -

System.out.println("Dentro de nuestra funcion tenemos valores definidos que son de 0 a 10 y tendremos que hayar los METODOS DE APROXIMACIONES SUCESIVAS");

System.out.println("las formulas dadas para encontrar x es 0+10/2=5 entonces x=5, tambien dada la ecuacion preestablecida de f(x)=-0.5x^2+2.5+4.5=0"); System.out.println("Haremos la simplificacion y desarrollo de la ecuacion dandonos g(x)=√5x+9, en la cual x será 5 y asi obtendremos g(x) y el resultado");

System.out.println("muestra la nueva x y comenzaremos de nuevo g(x) hasta completar la sucesicionn que queramos");

System.out.println("");

// - BUCLE WHILE -

int i=0;

int c=0;

System.out.println("Ingrese cuantas veces quiere repetir esta aproximacion sucesiva");

i=leer.nextInt();

System.out.println("");

System.out.println("Dentro de nuestra primera sucesion los valores que tenemos son los siguientes:");

while (c<i) {

// - APROXIMACIONES SUCESIVAS -

x1=raiz;

g1=(5*x1)+9;

raiz=Math.sqrt(g1);

b1=raiz;

ep1=((b1-x1)*100)/b1;

System.out.println("X es igual a: "+x1);

System.out.println("En g(x) sustituyendo en √5x+9, da como resultado: "+raiz);

System.out.println("El error porcentual es = |valor actual-valoranterior(100)|/valor actual: "+ep1+"%");

System.out.println("");

c++;

}

Codigo de biseccion ejercicio 2

package biseccion2;

import java.util.Scanner;

public class Biseccion2 {

Scanner Scanner = new Scanner (System.in);

public static void main(String[] args) {

float n1,n2,n3,n4;

System.out.println("Nuestra funcion Y= 4x^2-5x tiene como valores definidos");

System.out.println("Xa= 1 y Xb= 1.6");

// - PRIMERA ITERACION -

n1=1;

n2=2;

float nu2= 1.6f;

System.out.println("la formula para crear la iteracion es Xr= Xa+Xb/2");

n3=n1+nu2;

n4=n3/n2;

System.out.println("Sustituyendo la iteracion #1 es: "+n4);

System.out.println("");

// - SEGUNDA ITERACION -

float a1,a2,a3,a4;

a1=1;

a2=2;

float aa2= 1.3f;

System.out.println("la formula para la proxima iteracion es Xr= Xa+Xb/2");

System.out.println("Aqui los valores son Xa= 1 y Xb= 1.3");

a3=a1+aa2;

a4=a3/a2;

System.out.println("Sustituyendo la iteracion #2 es: "+a4);

System.out.println("");

// - TERCERA ITERACION -

float b2,b3,b4;

float bb1=1.15f;

b2=2;

float bb2=1.3f;

System.out.println("la formula para la proxima iteracion es Xr= Xa+Xb/2");

System.out.println("Aqui los valores son Xa= 1.15 y Xb= 1.3");

b3=bb1+bb2;

b4=b3/b2;

System.out.println("Sustituyendo la iteracion #3 es: "+b4);

System.out.println("");

// - CUARTA ITERACION -

float c2,c3,c4;

float cc1=1.225f;

c2=2;

float cc2= 1.3f;

System.out.println("la formula para la proxima iteracion es Xr= Xa+Xb/2");

System.out.println("Aqui los valores son Xa= 1.225 y Xb= 1.3");

c3=cc1+cc2;

c4=c3/c2;

System.out.println("Sustituyendo la iteracion #4 es: "+c4);

System.out.println("");

// - QUINTA ITERACION -

float d2,d3,d4;

float dd1=1.225f;

d2=2;

float dd2= 1.2625f;

System.out.println("la formula para la proxima iteracion es Xr= Xa+Xb/2");

System.out.println("Aqui los valores son Xa= 1.225 y Xb= 1.2625");

d3=dd1+dd2;

d4=d3/d2;

System.out.println("Sustituyendo la iteracion #5 es: "+d4);

System.out.println("");

}

Codigo de biseccion ejercicio 1

package biseccion1;

import java.util.Scanner;

public class Biseccion1 {

Scanner Scanner = new Scanner (System.in);

public static void main(String[] args) {

float n1,n2,n3,n4;

System.out.println("Nuestra funcion Y= x^4-2 tiene como valores definidos");

System.out.println("Xa= 1 y Xb= 0");

// - PRIMERA ITERACION -

n1=1;

n2=2;

float nu2= 0f;

System.out.println("la formula para crear la iteracion es Xr= Xa+Xb/2");

n3=n1+nu2;

n4=n3/n2;

System.out.println("Sustituyendo la iteracion #1 es: "+n4);

System.out.println("");

// - SEGUNDA ITERACION -

float a1,a2,a3,a4;

a1=0.5f;

a2=2;

float aa2= 1f;

System.out.println("la formula para la proxima iteracion es Xr= Xa+Xb/2");

System.out.println("Aqui los valores son Xa= 0.5 y Xb= 1");

a3=a1+aa2;

a4=a3/a2;

System.out.println("Sustituyendo la iteracion #2 es: "+a4);

System.out.println("");

// - TERCERA ITERACION -

float b2,b3,b4;

float bb1=0.75f;

b2=2;

float bb2=1f;

System.out.println("la formula para la proxima iteracion es Xr= Xa+Xb/2");

System.out.println("Aqui los valores son Xa= 0.75 y Xb= 1");

b3=bb1+bb2;

b4=b3/b2;

System.out.println("Sustituyendo la iteracion #3 es: "+b4);

System.out.println("");

// - CUARTA ITERACION -

float c2,c3,c4;

float cc1=0.75f;

c2=2;

float cc2= 0.875f;

System.out.println("la formula para la proxima iteracion es Xr= Xa+Xb/2");

System.out.println("Aqui los valores son Xa= 0.75 y Xb= 0.87");

c3=cc1+cc2;

c4=c3/c2;

System.out.println("Sustituyendo la iteracion #4 es: "+c4);

System.out.println("");

// - QUINTA ITERACION -

float d2,d3,d4;

float dd1=0.75f;

d2=2;

float dd2= 0.812f;

System.out.println("la formula para la proxima iteracion es Xr= Xa+Xb/2");

System.out.println("Aqui los valores son Xa= 0.75 y Xb= 0.81");

d3=dd1+dd2;

d4=d3/d2;

System.out.println("Sustituyendo la iteracion #5 es: "+d4);

System.out.println("");

// - SEXTA ITERACION -

float e2,e3,e4;

float ee1=0.71f;

e2=2;

float ee2= 0.81f;

System.out.println("la formula para la proxima iteracion es Xr= Xa+Xb/2");

System.out.println("Aqui los valores son Xa= 0.71 y Xb= 0.81");

e3=ee1+ee2;

e4=e3/e2;

System.out.println("Sustituyendo la iteracion #5 es: "+e4);

System.out.println("");

}

jueves, 16 de marzo de 2023

aproximaciones sucesivas

El moldeamiento es una técnica que se utiliza para favorecer el aprendizaje, sobre todo en menores con necesidades especiales. Fue descrita por primera vez por el psicólogo B. F. Skinner, padre del condicionamiento operante, y supuso un hito fundamental en el desarrollo de este paradigma conductista.

En este artículo explicaremos qué es el moldeamiento, también llamado “método de las aproximaciones sucesivas” debido a que consiste básicamente en reforzar una conducta de forma selectiva para que acabe adoptando una topografía y una función determinadas. También hablaremos de algunas de las técnicas operantes que se suelen usar junto con el moldeamiento.

¿Qué es el moldeamiento?

El moldeamiento es un paradigma de aprendizaje que se enmarca en el condicionamiento operante. En el contexto del análisis de conducta aplicado, que fue desarrollado por Burrhus Frederick Skinner, el moldeamiento de comportamientos se lleva a cabo normalmente a través del método de reforzamiento diferencial por aproximaciones sucesivas.

Estos procedimientos se basan en la modificación progresiva de una respuesta existente en el repertorio conductual del sujeto que aprende. Al reforzar de forma selectiva conductas cada vez más parecidas a la que se pretende establecer, estas se fortalecen mientras que las que son menos precisas tienden a extinguirse a causa de la falta de contingencia con refuerzos.

Así, el mecanismo fundamental de estas técnicas conductuales es el refuerzo, en particular el de tipo diferencial. Desde mediados del siglo XX sabemos que resulta más eficaz focalizar los procesos de instrucción en el reforzamiento de conductas deseables que en el castigo de otras incorrectas, tanto por cuestiones éticas como por otras puramente prácticas.

El moldeamiento es una de las técnicas operantes que sirven para desarrollar conductas. En este sentido es similar al encadenamiento, en el cual el aprendizaje consiste en combinar comportamientos sencillos presentes en el repertorio del sujeto con el objetivo de formar cadenas conductuales complejas, como arrancar un vehículo o tocar un instrumento musical.

El método de aproximaciones sucesivas

Para aplicar el moldeamiento y el método de aproximaciones sucesivas es necesario en primer lugar determinar cuál es la conducta final que el sujeto deberá aprender a ejecutar. A continuación se evalúa su repertorio de respuestas, por lo general a través de tests conductuales, para identificar una que pueda ser un buen punto de partida para el aprendizaje.

En concreto, el objetivo es seleccionar una conducta que el sujeto pueda llevar a cabo sin problema y que se parezca lo más posible a la respuesta objetivo, tanto en su faceta topográfica (p. e. tipo de movimientos musculares implicados) como en la funcional; éste término hace referencia a la meta o función que cumple un comportamiento determinado.